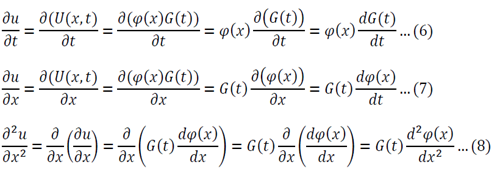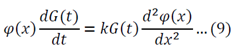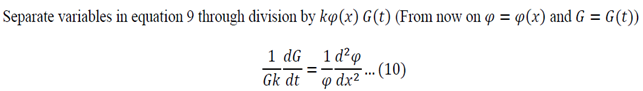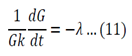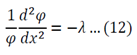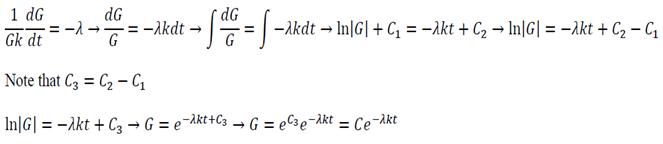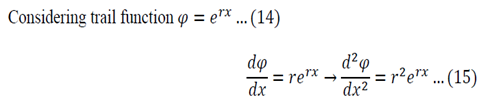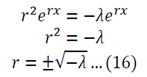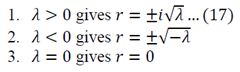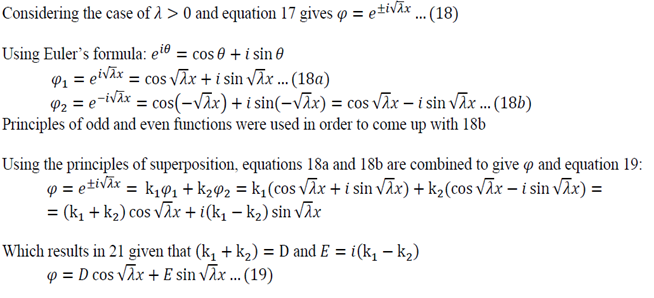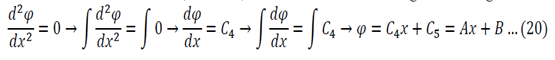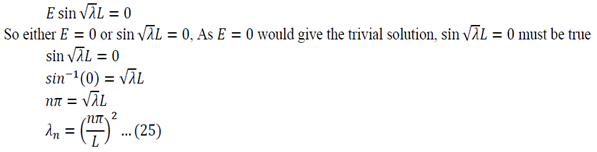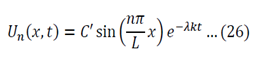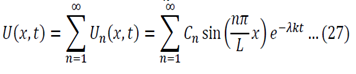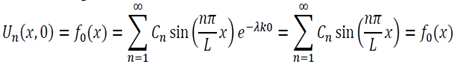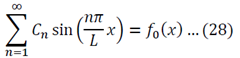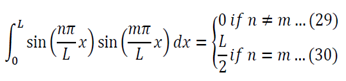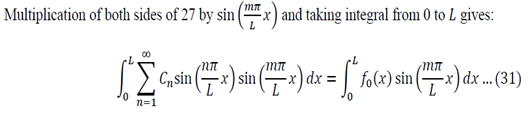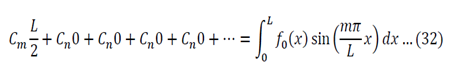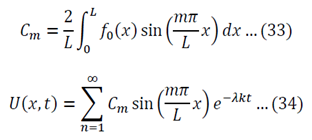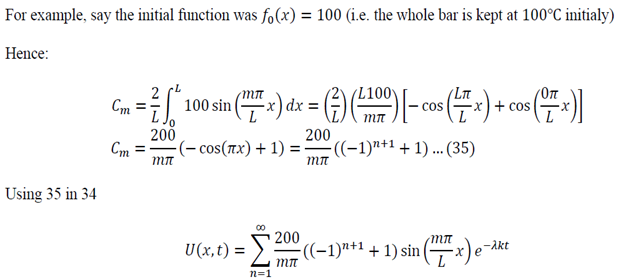I received a great tutorial on how to apply separation of variables to solve a partial differential equation. I copied some of the equations as images because my generic editor cannot handle some symbols. The example is the following:
A uniform rod of length L with Finite Ends at Zero Temperature.
Equation given:
For 0 < x < L and t >= 0
Boundary Conditions:
- U(0, t) = 0 … (2)
- U(L,t) = 0 … (3)
Initial Conditions – U(x,o) = fo(x) … (4)
- The PDE is linear and homogeneous
- The boundary conditions are also linear and homogeneous
Separation of variables:
Adjust 5 so that it can be substituted into 1:
Substitute 6 and 8 into 1:
Function of only time = Function of only space
Both sides of the equation must equal to the same constant, called a separation constant. We get:
And
Equation 11 is the time depended equation and will be solved first. This is a first order linear homogeneous ODE and can be solved using the method of separation of variables.
The final solution will then be:
Analysis of possible values of lambda:
- If lambda > 0 the temperature will exponentially decay with time
- If lambda < 0 the temperature will exponentially increase with time
- If lambda = 0 the temperature will stay constant
Only lambda => 0 makes sense as the temperature is not meant to grow to infinity.
Equation 12 is the space dependent equation. As equation 12 is a linear, second order, homogeneous ODE with constant coefficients, a method of constant coefficients can be used in order to solve that equation.
Substitution of 14 and 15 into 12 gives:
Equation 16 has numerous solutions, which all depend on the value of lambda:
Evaluate each of the cases
Lambda > 0
Lambda = 0
The solution of r=0 can be used here, or double integration can be used to solve equation 12
Substitution of equations 19, 20 and 13 into equation 5 gives the following general solution:
The boundary conditions now have to be applied:
Lambda > 0
Using Equation 22 in 19:
Using Equation 23 in 19:
Solving Equation 24:
Lambda is now written with a subscript n as it could take on multiple values due to infinite number of possible solutions of the sin function.
Lambda = 0
Application of 22 in 20:
Application of 23 in 20:
So either L is zero or A is zero. Having zero length defeats the purpose of the problem so A = must be true.
Using all the values determined from the boundary conditions in equation 21:
Where C’ = CE
We now use the initial conditions and get:
So then:
We can apply the following identity:
Using equations 29 and 30, the left side of 31 becomes:
To generalize: