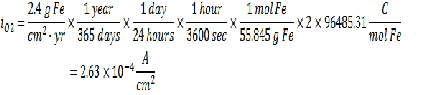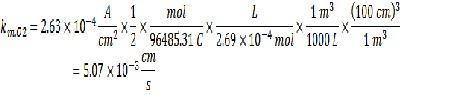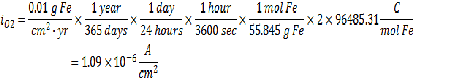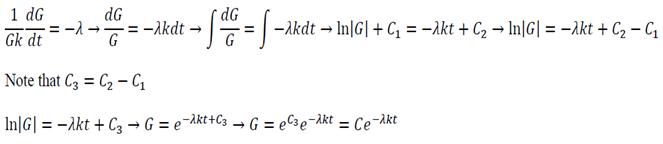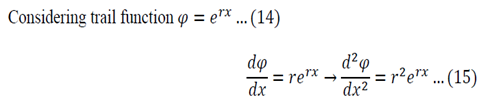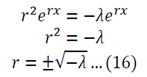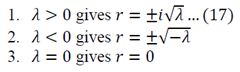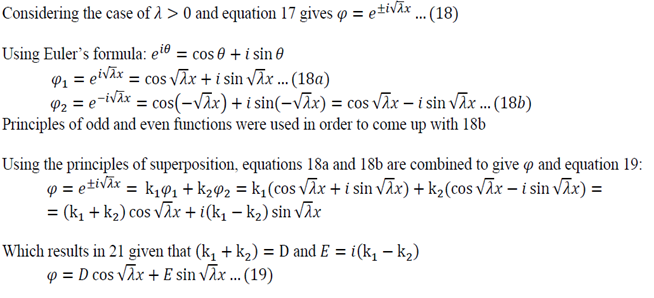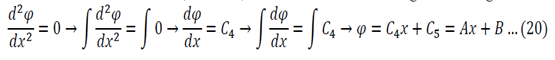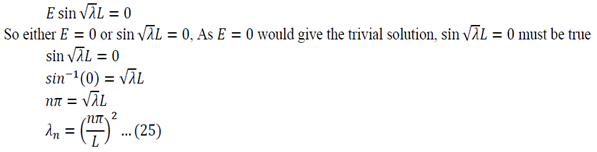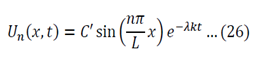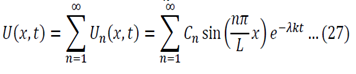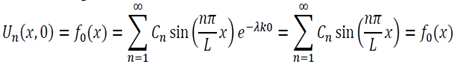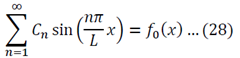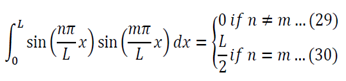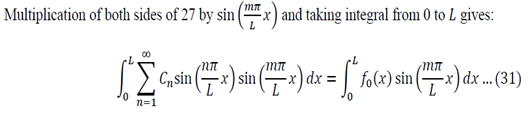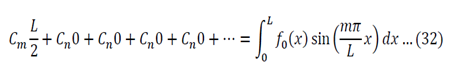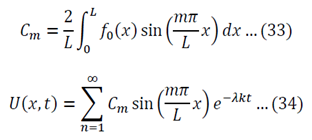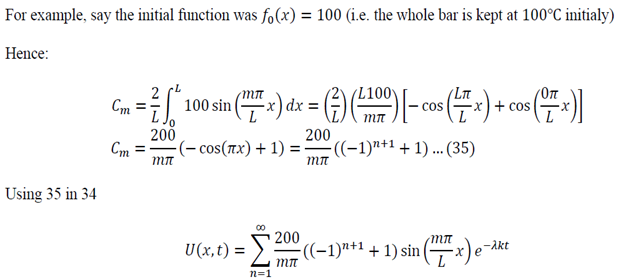Corrosion in a tank

One of the most common corrosion problems you will be asked to solve is how a tank, open to the atmosphere, corrodes and how you can control the rate of corrosion by simply covering the tank and regulating the pressure. Here is what is usually given:

T = 25^oC

P = 1 atm

Corrosion Rate = 2.4 g Fe/cm²-yr

Say that O2 reduction is limited by mass transfer of dissolved O2 to the tank wall and the solubility of dissolved oxygen can be related to its partial pressure:

C_O2 = 1.28x10^-3 P_O2

The partial pressure is in atm and the concentration is in mol/L. The oxidation of Fe^o is kinetically controlled in the Tafel region:

i_O = 0.8x10^-8 amp/cm²

Tafel Slope = 1/120 mV^-1

n_e = 1

Acceptable Corrosion Rate = 0.01 g Fe/cm²-yr

C_Fe2+ = 10^-6 mol/L at all times

Fe^o -> Fe²⁺ + 2e^-, -0.440 V_SHE

And you are asked to determine the total pressure the headspace should be evacuated to to attain the acceptable corrosion rate.

Solution:

You are given that the O2 reduction is mass transfer limited so right away you can modify your general equation from:

To:

From the given information you can find the concentration of dissolved oxygen in the bulk as well as the current from the Faraday’s law. Please see my earlier posts for more information on how to use Faraday’s to calculate current given a deposition rate.

From the given relationship between pressure and concentration, you can determine the bulk concentration of dissolved oxygen:

Now that you have all the required information, you can calculate the k_m value.

The next step is to determine the current density at the acceptable corrosion rate using the same line calculation as before:

Looking at the mass transfer limitation equation, we only have 1 unknown – the bulk concentration of dissolved oxygen, which is calculated via:

Great, now we can use the given relationship for partial pressure of oxygen and concentration to determine the partial pressure of oxygen in the headspace:

This is not the end, because oxygen only accounts for 21% of the composition of air, so the total headspace pressure has to be:

I apologize how bad some of the equations look. I really have to look into finding a new blog editor. If this has helped you in any way, please click on some of the ads.

Technorati Tags: Corrosion,tank corrosion,tank,oxygen

Partial Differential Equations – Separation of Variables

 

I received a great tutorial on how to apply separation of variables to solve a partial differential equation. I copied some of the equations as images because my generic editor cannot handle some symbols. The example is the following:

A uniform rod of length L with Finite Ends at Zero Temperature.

Equation given:

For 0 < x < L and t >= 0

Boundary Conditions:

• U(0, t) = 0 … (2)
• U(L,t) = 0 … (3)

Initial Conditions – U(x,o) = fo(x) … (4)

• The PDE is linear and homogeneous
• The boundary conditions are also linear and homogeneous

Separation of variables:

Adjust 5 so that it can be substituted into 1:

Substitute 6 and 8 into 1:

Function of only time = Function of only space

Both sides of the equation must equal to the same constant, called a separation constant. We get:

 

And

Equation 11 is the time depended equation and will be solved first. This is a first order linear homogeneous ODE and can be solved using the method of separation of variables.

The final solution will then be:

Analysis of possible values of lambda:

1. If lambda > 0 the temperature will exponentially decay with time
2. If lambda < 0 the temperature will exponentially increase with time
3. If lambda = 0 the temperature will stay constant

Only lambda => 0 makes sense as the temperature is not meant to grow to infinity.

Equation 12 is the space dependent equation. As equation 12 is a linear, second order, homogeneous ODE with constant coefficients, a method of constant coefficients can be used in order to solve that equation.

Substitution of 14 and 15 into 12 gives:

Equation 16 has numerous solutions, which all depend on the value of lambda:

Evaluate each of the cases

Lambda > 0

 

Lambda = 0

The solution of r=0 can be used here, or double integration can be used to solve equation 12

Substitution of equations 19, 20 and 13 into equation 5 gives the following general solution:

The boundary conditions now have to be applied:

Lambda > 0

Using Equation 22 in 19:

Using Equation 23 in 19:

Solving Equation 24:

Lambda is now written with a subscript n as it could take on multiple values due to infinite number of possible solutions of the sin function.

Lambda = 0

Application of 22 in 20:

Application of 23 in 20:

So either L is zero or A is zero. Having zero length defeats the purpose of the problem so A = must be true.

Using all the values determined from the boundary conditions in equation 21:

Where C’ = CE

We now use the initial conditions and get:

So then:

We can apply the following identity:

Using equations 29 and 30, the left side of 31 becomes:

To generalize:

Technorati Tags: Differential Equations,Partial Differential Equations,Separation of Variables,Mathematics,Math Examples